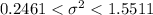Question

A company produces a women's bowling ball that is supposed to weigh exactly 14 pounds. Unfortunately, the company has a problem with the variability of the weight. In a sample of 11 of the bowling balls the sample standard deviation was found to be 0.71 pounds. Construct a 95% confidence interval for the variance of the bowling ball weight. Assume normality.

Answer 1

Answer:
`0.2461<\sigma^2<1.5511`

Explanation:

Given : A company produces a women's bowling ball that is supposed to weigh exactly 14 pounds.

Sample size : n=11

Degree of freedom =n-1=10

Sample standard deviation : s= 0.71 pounds

Significance level for 95% confidence interval :
`\alpha=1-0.95=0.05`

We assume that the bowling ball weight is normally distributed.

Using chi-square distribution table, the required critical values are :-

`\chi^2_(df, \alpha/2)=20.48`

`\chi^2_(df, 1-\alpha/2)=3.25`

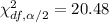
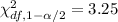
Then, the 95% confidence interval for the variance of the bowling ball weight will be :

`(s^2(n-1))/(\chi_(\alpha/2))<\sigma^2<(s^2(n-1))/(\chi_(1-\alpha/2))`

`=((0.71)^2(10))/(20.48)<\sigma^2<((0.71)^2(10))/(3.25)\\\\=0.2461<\sigma^2<1.5511`

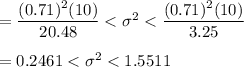
∴ The 95% confidence interval for the variance of the bowling ball weight will be :
`0.2461<\sigma^2<1.5511`