Question

A manufacturer of chocolate chips would like to know whether its bag filling machine works correctly at the 420.0420.0 gram setting. It is believed that the machine is underfilling the bags. A 3333 bag sample had a mean of 417.0417.0 grams. A level of significance of 0.010.01 will be used. State the hypotheses. Assume the variance is known to be 576.00576.00. Enter the hypotheses:

Answer 1

`H_(0)` : μ=420 gram

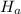`H_(a)` : μ≠420 gram

we fail to reject the null hypothesis at 0.01 significance

Explanation:

Let μ be the mean value for the bag filling machine. Then

`H_(0)` : μ=420 gram

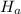`H_(a)` : μ≠420 gram

z-score of the sample mean can be calculated as:

z=
`(X-M)/((s)/(√(N) ) )` where

• X is the sample mean (417)
• M is the mean assumed in null hypothesis (420)
• s is the standard deviation (
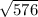  `√(576)` = 24)
• N is the sample size (33)

then z=
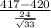`(417-420)/((24)/(√(33) ) )` =-0.718

since p(z)= 0.858 > 0.01 we fail to reject the null hypothesis.