Question

A 30-mm-thick plate made of low carbon steel is to be reduced to 25 mm in one pass in a rolling operation. As the thickness reduce the plate widens by 4%. Yield strength ofthe steel =174 MPa, and tensile strength = 290 MPa. The entrance speed of the plate-77 m/min. Roll radius 300 mm, and rotational speed 45 rev/min. Determine: (e) the minimum required coefficient of friction that would make this rolling operation possible (b) exit velocity of the plate (c) forward slip. WRITE YOUR ANSWERS HERE: a) Minmum required coefficient of friction b) Exit velocity of the plate c) Forward slip, s.

Answer 1

Given that

h = 30 mm

h' = 25 mm

Δh= 30 - 25 = 5 mm

Initial width = b

Final width = 1.04 b

Roll radius, r = 300 mm

Inlet velocity Vi = 77 m/min

N = 45 RPM

a)

As we know that

Δh = μ² .r

μ = Coefficient of friction

r = roll radius

By putting the values

Δh = μ² .r

5 = μ² x 300

μ=0.12

b)

From continuity equation

Ai Vi=
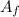`A_f` Vf

Ai = Inlet area, Vi= inlet velocity

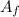`A_f` = exit area, Vf= exit velocity

b x h x Vi= 1.04 b x h' x Vf

b x 30 x 77 = 1.04 b x 25 x Vf

Vf=88.84 m/min

c)

Forward slip S given as

`S=(V_f)/(V)-1`

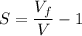
V= Roller speed

We know that

`V=(2\pi rN)/(60)m/s`

`V=(2\pi * 0.3* 45)/(1)`

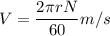
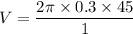
V=84.82 m/min

`S=(V_f)/(V)-1`

`S=(88.84)/(84.82)-1`

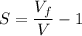
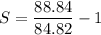
S=0.047