Question

A circular loop of wire having a radius of 5.58 cm carries a current of 0.230 A. A vector of unit length and parallel to the dipole moment of the loop is given by 0.60 – 0.80. If the loop is located in a uniform magnetic field given by = (0.140 T) + (0.109 T), find (a) the x-component, (b) the y-component, and (c) the z-component of the torque on the loop and (d) the magnetic potential energy of the

Answer 1

see explanation

Step-by-step explanation:

Given quantities:

radius = r = 0.0558 [m]

current = I = 0.23 [A]

`\vec{B} = <0.14[T] \hat i + 0.109[T] \hat j >`

Now we solve this by obtaining the torque acting on the dipole

`\tau = M * B`

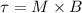
We obtain the magnetic moment vector M, first, |M| is defined as
`M = IA`, where A is the cross-section area of the loop which is
`A = \pi r^2=\pi (0.0558)^2= 0.00978 [m^2]` then

`|M| = 0.23*0.00978 = 0.00225 [A/m^2]`

now the magnetic moment vector is equal to the magnetic dipole moment vector multiplied the magnitude we just obtained
`\vec{M} = M \hat M`

`= 0.00225 *<0.6 \hat i - 0.8 \hat j>`

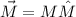
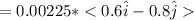
Now:

a )
`\tau = M * B`

b)
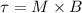
`U = -M \cdot B`

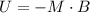
a) the determinant gives us:

`<0 \hat i,0 \hat j,0.00039915 \hat k>`

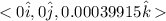
b) the dot product gives =
`-1*-7.2*10^(-6) = 7.2*10^(-6)[J]`