Question

A company is considering buying a new piece of machinery. A 10% interest rate will be used in the computations. Two models of the machine are available.

Machine I

Initial cost:$80,000

End -of -useful –life Salvage value, S: 20,000

Annual operating cost 18,000

Useful life, in years 20

Machine II

Initial cost: $100,000

End -of -useful –life Salvage value, S: 25,000

Annual operating cost: 15,000 first 10 years, 20,000 thereafter

Useful life, in years: 25

(a) Determine which machine should be purchased, based on equivalent uniform annual cost.

(b) What is the capitalized cost of Machine I?

(c) Machine I is purchased and a fund is set up to replace Machine i at the end of 20 years. Compute the required uniform annual deposit.

(d) Machine I will produce an annual saving of material of $28,000. What is the rate of return if Machine I is installed?

(e) What will be the book value of Machine I after 2 years, based on sum -of -years' -digits depreciation?

(f) What will be the book value of Machine II after 3 years, based on double declining balance depreciation?

Answer 1

The best production method is determined by calculating the total costs of labor and capital. With labor costing $100/unit, Method 1 is the cheapest at $9,000. If the labor cost increases to $200/unit, Method 1 and Method 2 are tied as the cheapest, both costing $18,000.

Step-by-step explanation:

To determine the best production method, we need to calculate the total cost for each method, factoring in the cost of labor and capital. For Method 1, assuming labor costs $100/unit and capital costs $400/unit, the calculation is 50 units of labor × $100/unit + 10 units of capital × $400/unit, which equals $9,000. For Method 2, the calculation is 20 units of labor × $100/unit + 40 units of capital × $400/unit, which equals $18,000. For Method 3, the calculation is 10 units of labor × $100/unit + 70 units of capital × $400/unit, which equals $29,000. With these costs, Method 1 is the cheapest.

When the cost of labor rises to $200/unit, we recalculate. For Method 1, the new cost is 50 units of labor × $200/unit + 10 units of capital × $400/unit, resulting in $18,000. For Method 2, the cost is 20 units of labor × $200/unit + 40 units of capital × $400/unit, still $18,000. For Method 3, the calculation is 10 units of labor × $200/unit + 70 units of capital × $400/unit, which remains $29,000. With these new costs, both Method 1 and Method 2 are now the cheapest, and either could be chosen based on other factors.

Answer 2

Machine I

capitalized cost: 230,271.28

EAC: $ 27,047.58

Machine II

EAC: $ 27,377.930

As Machine I cost per year is lower it is better to purchase that one.

Annual deposits to purchase Machine I in 20 years: $ 1,396.770

return of machine I with savings of 28,000 per year: 10.51%

Step-by-step explanation:

WE calculate the present worth of each machine and then calculate the equivalent annual cost:

MACHINE 1

Operating cost:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 18,000

time 20

rate 0.1

`18000 * (1-(1+0.1)^(-20) )/(0.1) = PV\\`

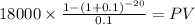
PV $153,244.1470

Salvage value:

`(Maturity)/((1 + rate)^(time) ) = PV`

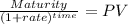
Maturity $20,000.0000

time 20.00

rate 0.1

`(20000)/((1 + 0.1)^(20) ) = PV`

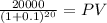
PV 2,972.87

Total: -80,000 cost - 153,244.15 annual cost + 2,972.87 salvage value:

Total: 230,271.28

`PV / (1-(1+r)^(-time) )/(rate) = C\\`

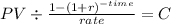
Present worth $(230,271.28)

time 20

rate 0.1

`-230271.28 / (1-(1+0.1)^(-20) )/(0.1) = C\\`

C -$ 27,047.578

Fund to purchase in 20 years:

`FV / ((1+r)^(time) -1)/(rate) = C\\`

FV $80,000.00

time 20

rate 0.1

`80000 / ((1+0.1)^(20) -1)/(0.1) = C\\`

C $ 1,396.770

IF produce a 28,000 savings:

we must solve using a financial calcualtor for the rate at which the capitalized cost equals 28,000

`PV / (1-(1+r)^(-time) )/(rate) = C\\`

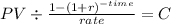
PV $230,271.28

time 20

rate 0.105126197

`230271.28 / (1-(1+0.105126197287798)^(-20) )/(0.105126197287798) = C\\`

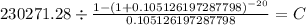
C $ 28,000.000

rate of 0.105126197 = 10.51%

Machine II

100,000 cost

25,000 useful life

15,000 operating cost during 10 years

20,000 for the next 15 years

Present value of the operating cost:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 15,000

time 10

rate 0.1

`15000 * (1-(1+0.1)^(-10) )/(0.1) = PV\\`

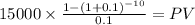
PV $92,168.5066

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 20,000

time 15

rate 0.1

`20000 * (1-(1+0.1)^(-15) )/(0.1) = PV\\`

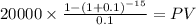
PV $152,121.5901

in the timeline this is at the end of the 10th year we must discount as lump sum for the other ten years:

`(Maturity)/((1 + rate)^(time) ) = PV`

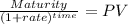
Maturity $152,121.5901

time 10.00

rate 0.1

`(152121.590126167)/((1 + 0.1)^(10) ) = PV`

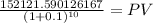
PV 58,649.46

salvage value

`(Maturity)/((1 + rate)^(time) ) = PV`

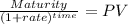
Maturity $25,000.0000

time 25.00

rate 0.1

`(25000)/((1 + 0.1)^(25) ) = PV`

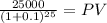
PV 2,307.40

Total cost: 100,000 + 92,168.51 + 58,649.46 - 2,307.40 = $248,510.57

`PV / (1-(1+r)^(-time) )/(rate) = C\\`

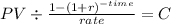
PV $248,510.57

time 25

rate 0.1

`248510.57 / (1-(1+0.1)^(-25) )/(0.1) = C\\`

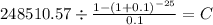
C $ 27,377.930