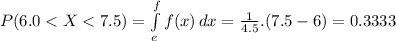Answer:
I.
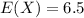
σ = 1.299
II.
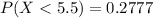
III.
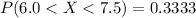
Step-by-step explanation:
Let's start defining the random variable X.
X : ''The data transfer rate that a phone experiences''
X is a continuous random variable.
X ~ U (4.25,8.75)
For a uniformly distributed random variable the probability density function is :
X ~ U [a,b]
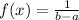 if x ∈ (a,b)
if x ∈ (a,b)
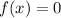 if x ∉ (a,b)
if x ∉ (a,b)
In this exercise :
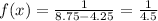 if x ∈ (4.25,8.75)
if x ∈ (4.25,8.75)
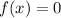 if x ∉ (4.25,8.75)
if x ∉ (4.25,8.75)
I. The mean of a uniformly distributed random variable is :
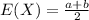

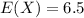
The variance of a uniformly distributed random variable is :
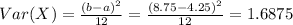
For the standard deviation :

σ = 1.299
II.
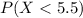
If c = - ∞ and d = 5.5 ⇒


III.
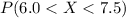
If e = 6.0 and f = 7.5 ⇒