Question

A 1200-ft equal-tangent crest vertical curve is currently designed for 50 mi/h. A civil engineering student contends that 60 mi/h is safe in a van because of the higher driver’s-eye height. If all other design inputs are standard, what must the driver’s-eye height (in the van) be for the student’s claim to be valid?

Answer 1

8.95ft

Step-by-step explanation:

In order to develop this problem it is necessary to consider two concepts:

The first is the design of vertical curves through the general equation for the length of a curved vertical crest in terms of algebraic differences in grades. The second is the Design Controls for Crest vertical curves table (I attach a table at the end).

The aforementioned equation is given by:

`L = (AS^2)/(200(√(h_1)+√(h_2))^2)`

Where,

L = leght of vertical curve

S = Sight distance

A = Algebraic difference in grades

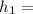`h_1 =`Height of eye above roadway

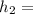`h_2 =`height of object above roadway surface

From the table we know that for design speed of 60 mi/h the S is 570 ft, while the value of the rate of vertival curve K, for design speed of 50mi/h is 84.

Then we can calculate the Algebraic difference in grades through:

`A= (L)/(K)`

`A = (1200)/(84)`

`A = 14.285`

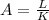
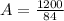
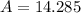
Applying the equation to find
`h_1` we have:

`L = (AS^2)/(200(√(h_1)+√(h_2))^2)`

`1200 = (14.32(570)^2)/(200(√(h_1)+√(2))^2)`

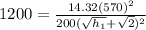
Solving for
`h_1`

`h_1 = 8.95ft`

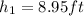
Therefore the height of the driver's eye is 8.95ft