Question

A potter’s flywheel is made of a 5.00-cm-thick, round slab of concrete that has a mass of 60.0 kg and a diameter of 35.0 cm. This disk rotates about an axis that passes through its center, perpendicular to its round area. Calculate the angular speed of the slab about its center if the rotational kinetic energy is 15.0 J. Express your answer in both rad/s and rev/min.

Answer 1

5.71 rad/s , 54.55 rev/min

Step-by-step explanation:

mass of disc, m = 60 kg

diameter of disc = 35 cm

radius of disc, r = 17.5 cm

Rotational kinetic energy, K = 15 J

Let I be the moment of inertia of the disc and ω be the angular speed of the disc.

The moment of inertia of the disc is given by

`I = (1)/(2)mr^(2)`

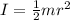
I = 0.5 x 60 x 0.175 x 0.175 = 0.92 kg m^2

Kinetic energy

`K = (1)/(2)I\omega ^(2)`

`15 = (1)/(2)* 0.92\omega ^(2)`

`\omega ^(2)=32.6`

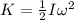
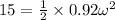
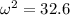
ω = 5.71 rad/s

ω = 5.71 / 2π rev /s

ω = 0.909 rev /s

ω = 0.909 x 60 rev / min = 54.55 rev/min