Question

A professor would like to estimate the average number of hours his students spend studying for his class. He wants to estimate μwith 99% confidence and with a margin of error of at most 2 hours. From past experience he knows the standard deviation of number of hours spent studying to be 8 hours. How many students need to be surveyed to meet these requirements? A. 106B. 105C. 107D. 108

Answer 1

n=106.1≅106

Option A which is 106 is correct

Explanation:

In order to find the number of students need to be surveyed to meet the requirements we will use the following formula:

`n=(Z^2*S^2)/(E^2)`

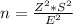
where:

n is the number of students need o be surveyed

Z is the distribution

S is the standard Deviation

E is the error Margin

Now:

S=8 ,E=2, CI= 99% or 0.99

For Z we need to find Alpha/2

Alpha=1-0.99

Alpha=0.01

Alpha/2=0.005 or 0.5%

From the cumulative Standard Distribution Table:

Z at alpha/2 =2.576

n= (2.576^2* 8^2)/2^2

n=106.1≅106

Option A which is 106 is correct