Question

How many different ways are there to arrange the letters A, B, A, and B? 4 6 8 16

Answer 1

There are 6 different possible arrangements of letters A, B, A, B.

Solution:

Need to determine different ways to range letters A, B, A and B.

Using the theorem which says that the number of permutation of n alphabets, where
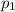`p_1` number of alphabets of one kind and
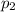`p_2` is number of alphabets of second kind is given by following formula.

Number of possible arrangements
`=(n !)/(p_(1) ! * p_(2) !) \rightarrow(1)`

In our case total number of alphabets = n = 4

Number of letter A =
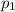`p_1` = 2

Number of letter B =
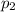`p_2` = 2

Using (1), we get

Number of possible arrangements of A, B, A, B
`=(4 !)/(2 ! * 2 !)=(4 * 3 * 2 * 1)/(2 * 1 * 2 * 1)=3 * 2=6`

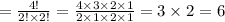
Hence there are 6 different possible arrangements of letters A, B, A, B.