Answer :
42.26 mph (approx)
Explanation :
Given,
Fuel consumption = 500/x miles per gallon,
Speed = x miles per hour
Also, hourly cost = $2.80/gal,
So, fuel cost =
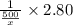
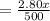 dollar per mile,
dollar per mile,
The driver earns $10 per hour.
So, labour cost = (10 dollars per hour) × (1/x hr per mile)
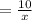 dollars per mile,
dollars per mile,
Thus, total cost,
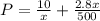
Differentiating with respect to x
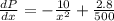
Again differentiating with respect to x,

When,
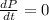
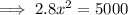
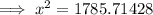
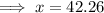
At x = 42.26,
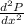 = positive.
= positive.
Hence, the speed would be 42.26 miles per hour.