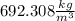Answer:
a)
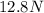
b)
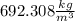
c)
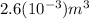
Step-by-step explanation:
Let's write the information given by the exercise.
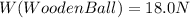
δ (Water) =
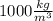
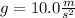
The buoyant force exerted by the water is :
E= V.δ.g
Where E is the buoyant force
V is the shifted volume of the fluid
δ is the fluid density
and g is the gravity acceleration.
We can write the following equation :
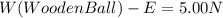
18.0 N - V.δ(water).g = 5.00 N
![13N=0.5[V(WoodenBall)]1000(kg)/(m^(3)).10(m)/(s^(2))](https://img.qammunity.org/2020/formulas/physics/college/chusnffv0squuyj6llfuatn2d10svzbmwq.png)
Let's remember that
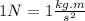
Therefore,
![13N=0.5[V(WoodenBall)].10000(N)/(m^(3))](https://img.qammunity.org/2020/formulas/physics/college/z2hdb738ndr5kgqfwcc0vzgxx6cb1x2a2v.png)

And that is the answer for c)
For a) we write
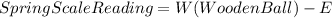
Spring scale reading = 18 N - 0.2 [V(Wooden ball)] . δ(water). g
![SpringScaleReading=18N-0.2[2.6(10^(-3))m^(3)].1000(kg)/(m^(3)).10(m)/(s^(2))](https://img.qammunity.org/2020/formulas/physics/college/8daa0rohc2hej2caurnrgerdi7kr5bc7tm.png)
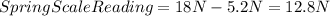
For a) The spring scale will read 12.8 N
b)

Where m(Wooden Ball) is the mass of the wooden ball.
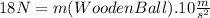
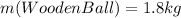
δ(Wooden ball) = m(Wooden ball) / V(Wooden ball)
δ(Wooden ball) = 1.8 kg /
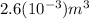
δ(Wooden ball) =