Answer:
C) 212nm
Step-by-step explanation:
For a thin layer of oil floating on water, there is an air-oil interface and oil-water interface. When light ray is incident on the thin layer of oil floating on the water, there is an interference which occur from the reflected ray from air-oil interface and oil-water interface. There is phase shift of 180° between the two rays due to reflections, then the interference is constructive.
Given:
Refractive index of oil (n₁) = 1.25
Refractive index of water (n₂) = 1.33
Refractive index of air (n₃) = 1.00
The wavelength of light = 530nm
Let thickness = t
The refractive index of air-to-oil
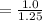
The refractive index of oil-to-water
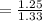
Since the refractive index of air-to-oil is lesser than the refractive index of oil-to-water, constructive interference occurs when:
2t = λ
n₁
t = λ
2 x n₁
t = 530
2 x 1.25
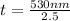
= 212nm
The minimum nonzero thickness of the oil in the region that strongly reflects green light = 212nm