Question

A truck with a mass of 1810 kg and moving with a speed of 16.0 m/s rear-ends a 673-kg car stopped at an intersection. The collision is approximately elastic since the car is in neutral, the brakes are off, the metal bumpers line up well and do not get damaged. Find the speed of both vehicles after the collision.

vcar = m/s
vtruck = m/s

Answer 1

velocity of truck = 7.32 m/s

velocity of truck = 23.32 m/s

Step-by-step explanation:

mass of truck, M = 1810 kg

initial velocity of truck, U = 16 m/s

mass of car, m = 673 kg

initial velocity of car, u = 0 m/s

Let the final speed of the car is v and the final speed of truck is V.

Use conservation of momentum

Momentum before collision = Momentum after collision

M x U + m x 0 = M x V + m x v

1810 x 16 + 0 = 1810 V + 673 v

28960 = 1810 V + 673 v .... (1)

As the collision is elastic, so the coefficient of restitution is 1.

By using the formula

`e=(v_(1)-v_(2))/(u_(2)-u_(1))`

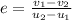
where, u1 be the initial velocity of truck, u2 be the initial velocity of the car, v1 be the final velocity of truck and v2 be the final velocity of car.

`1=\frac{V - v}}{0-U}`

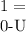
V - v = - U

V - v = - 16

v - V = 16

v = 16 + V

Substitute in equation (1), we get

28960 = 1810 V + 673 (16 + V)

28960 = 1810 V + 10768 + 673 V

18192 = 2483 V

V = 7.32 m/s

v = 16 + 7.32 = 23.32 m/s

Thus, the velocity of truck after collision is 7.32 m/s and the velocity of car after collision is 23.32 m/s.