Question

During the summer months Terry makes and sells necklaces on the beach. Last summer he sold the necklaces for $10 each and his sales averaged 20 per day. When he increased the price by $1, he found that the average decreased by two sales per day.

(a) Find the demand function (price p as a function of units sold x), assuming that it is linear. p(x) =_______
(b) If the material for each necklace costs Terry $6, what should the selling price be to maximize his profit? $________

Answer 1

given,

Let P₁ = $ 10 each and x₁ = 20 Per day

then P₂ = 10 + 1 = $11 each

average sale decreased by 2 sales per day

x₂ = 20 - 2 = 18 unit/day

a)

The demand function

`P(x) = P_1 + (P_2-P_1)/(x_2-x_1)(x-20)`

=
`10+ (11-10)/(18-20)(x-20)`

=
`10- (x-20)/(2)`

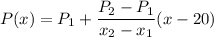
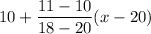
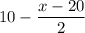
= 20 - 0.5 x

the demand function = P(x) = 20 - 0.5 x

b) The cost function C(x) = 6 x

The revenue function is R(x) = x P(x)

= x (20 - 0.5 x)

= 20 x - 0.5 x²

Marginal revenue R'(x) = 20 - x

Maximum Profit

C'(x) = R'(x)

6 = 20 - x

x = 14

P(x = 14) = 20 - 0.5 x 14

= 20 - 7

= 13

The selling price of maximum profit $13