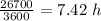Question

Arsenic diffusion in Si: Arsenic is diffused into a thick slice of silicon with no previous arsenic in it at 1100ºC. If the surface concentration of the arsenic is 5.0 × 1018 atoms/cm3 and its concentration at 1.2 µm below the silicon surface is 1.5 × 1016 atoms/cm3 , how long must be the diffusion time? (D = 3.0 × 10-14 cm2 /s for As diffusing in Si at 1100ºC.)

Answer 1

Diffusion time is 7.42 h

Solution:

As per the question:

Temperature, T =
`1100^(\circ)C`

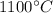
Surface concentration of arsenic,
`C_(S) = 5.0* 10^(18)\ atoms/cm^(3)`

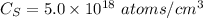
Surface concentration below Silicon surface,
`C_(x) = 1.5* 10^(16)\ atoms/cm^(3)`

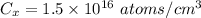
D =
`3.0* 10^(- 14)\ cm^(2)/s`

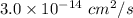
x =
`1.2\mu m = 1.2* 10^(- 4)\ cm`

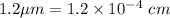
Initial concentration at t = 0,
`C_(o) = 0`

Now, by using Flick's second eqn:

`(C_(S) - C_(x))/(C_(x) - C_(o)) = erf((x)/(√(Dt)))`

Thus by putting appropriate values:

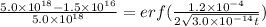
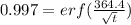`(5.0* 10^(18) - 1.5* 10^(16))/(5.0* 10^(18)) = erf(\frac{1.2* 10^(- 4)}{2\sqrt{3.0* 10^(- 14)t}})`

`0.997 = erf((364.4)/(√(t)))` (1)

Now,

`erf(z) = 0.997`

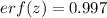
Now, from error function values tabulation:

For z = 2.0, erf(z) = 0.998

For z = 2.2, erf(z) = 0.995

Now,

With the help of linear interpolation method:

`(z - 2)/(2.2 - 2.0) = (0.997 - 0.995)/(0.998 - 0.995)`

z = 2.12

Now, using eqn (1) and above value:

`(364.4)/(√(t)) = 2.12`

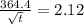
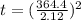`t = ((364.4)/(2.12))^(2)` = 26700 s

t =
`(26700)/(3600) = 7.42\ h`