Question

According to a dietary study, high sodium intake may be related to ulcers, stomach cancer, and migraine headaches. The human requirement for salt is only 220 milligrams per day, which is super passed in most of single servings of ready-to-eat cereals. A random sample of 20 similar servings of a certain cereal has a mean sodium content of 244 milligrams and standard deviation of 24.4 milligrams; does this suggest at the 0.05 level of significance that the average sodium content for a single serving of such a cereal is greater than 220 milligrams? Assume the distruibution of sodium content to be normal. Use Hypothesis testing to solve this question.

Answer 1

There is evidence at 95% level to support the claim that he average sodium content for a single serving of such a cereal is greater than 220 milligrams

Explanation:

Create hypothesis as

`H_0: \bar x =220 mg\\H_a: \bar x >220 mg/`

(Right tailed test at 5% significance level)

Mean difference =
`244-220 = 24mg`

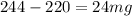
STd error =
`(s)/(√(n) ) \\=(24.4)/(√(20) ) \\=5.46`

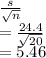
df =19

Test statistic t = mean diff/std error = 4.399

p value =0.0000155

Since p value is <0.05 reject null hypothesis.

There is evidence at 95% level to support the claim that he average sodium content for a single serving of such a cereal is greater than 220 milligrams