Question

The rate of transmission in a telegraph cable is observed to be proportional to x^22ln(1/x) where x is the ratio of the radius of the core to the thickness of the insulation (0

Answer 1

x = 0.606

Explanation:

Data provided in the question:

rate of transmission is proportional to
`x^(2)ln((1)/(x))`

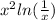
or

rate of transmission, R =
`C[x^(2)ln((1)/(x))]`

here, C is the proportionality constant

Now,

for point of maxima

differentiating the function with respect to 'x'

R' =
`(d(C[x^(2)ln((1)/(x))]))/(dx)`

using the product rule, we get\

R' =
`C[-2x^(1)\ln\left(x\right)-x^(1)]`

or

R' =
`C[-x^(1)\left(2\ln\left(x\right)+1\right)`

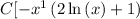
Now,

R' = 0 [for point of maxima]

OR

`C[-2x^(1)\ln\left(x\right)-x^(1)]` = 0

or

-x²¹ = 0 or
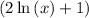`\left(2\ln\left(x\right)+1\right)` = 0

or

ln(x) =
`(-1)/(2)`

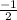
or

x = 0.606

Since,

0 < x < 1

Hence,

accepted value of x = 0.606