Question

An automobile manufacturer has given its van a 27.627.6 miles/gallon (MPG) rating. An independent testing firm has been contracted to test the actual MPG for this van since it is believed that the van has an incorrect manufacturer's MPG rating. After testing 210210 vans, they found a mean MPG of 28.028.0. Assume the population standard deviation is known to be 2.32.3. A level of significance of 0.050.05 will be used. State the null and alternative hypotheses.

Answer 1

The null and alternative hypothesis are:

`H_0: \mu\leq27.6\\\\H_1: \mu>27.6`

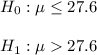
The null hypothesis can't be rejected.

Explanation:

In this case, we have to perform a hypothesis test of the mean, with known population standard deviation.

The sample has a size of n=210 and the mean of the sample is M=28.0.

The null and alternative hypothesis are:

`H_0: \mu\leq27.6\\\\H_1: \mu>27.6`

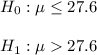
The significance level is 0.05.

In this test, if the null hypothesis is rejected, we can claim that the MPG are greater than what the manufacturer says.

The test statistic is:

`z=(M-\mu)/(\sigma)=(28.0-27.6)/(2.3)=(0.4)/(2.3)   =0.1739`

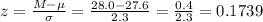
The P-value for z=0.1739 is
`P(z>0.1739)=0.431`.

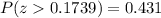The P-value is greater than the significance level, so the effect is not significant. The null hypothesis is fail to be rejected.