Question

A jewelry box with a square base is to be built with copper plated sides, nickel plated bottom and top, and a volume of 40cm^3. If nickel plating costs $2 per cm^2 and copper plating costs $1 per cm^2, find the dimensions of the box to minimize the cost of the materials.Please write out the process of solving this question in plain English

Answer 1

Length and width = 2.71 cm and height = 5.43 cm

Explanation:

Let the length of the jewelry box = x

Let the width = x [box is square, so length and width are same]

Let the height = y

Given volume = 40 cm³

Therefore, V = x²y

x²y = 40

y =
`(40)/(x^2)`

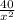
Cost of Nickle plating on top and bottom = $2 per cm²

Cost of copper plating on sides = $1 per cm²

Cost = 2(Areas of top and bottom) + 1(Areas of sides)

= 2(x² + x²) + 1(xy + xy + xy + xy)

= 4x² + 4xy

= 4x² = 4x
`((40)/(x))`

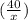
f(x) = 4x² +
`(160)/(x)`

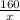
f'(x) = 8x -
`(160)/(x^2)=0`

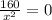
f"(x) =
`(8+320)/(x^3)>0`

f'(x) = 0

`(8x-160)/(x^2)=0`

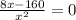
x³ = 20

x = ∛20

x = 2.71 cm

x²y = 40

∛400y = 40

y =
`\frac{40}{\sqrt[3]{400} }`

=
`(40)/(7.368)`

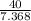
y = 5.4288 ≈ 5.43 cm

Length and width = 2.71 cm and height = 5.43 cm