Question

Bob is driving along a straight and level road toward a mountain. At some point on his trip, he measures the angle of elevation to the top of the mountain and finds it to be 25°11'. Find the height of the mountain to the nearest foot if Bob is 19,427.5 feet from the center of the mountain at the base.

a.9135 ft
b.9235 ft
c.91,351 ft
d.913,515 ft

Answer 1

Option A.

Explanation:

Distance between Bob and the center of the mountain at the base = 19,427.5 ft.

Angle of elevation to the top of the mountain = 25°11'

We know that

1 degree = 60 minutes

1/60 degree = 1 minute

`25^(\circ)11'=25^(\circ)+(11)/(60){\circ}\Rightarrow 25^(\circ)+0.183^(\circ)=25.183^(\circ)`

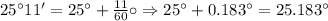
Let the height of the mountain be h.

In a right angled triangle

`\tan\theta = (opposite)/(adjacent)`

`\tan(25.183^(\circ)) = (h)/(19427.5)`

`\tan(25.183^(\circ))* 19427.5 = h`

`h=0.4702* 19427.5`

`h=9134.8105`

`h\approx 9135`

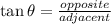
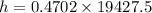
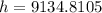
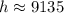
Therefore, the height of the mountain to the nearest foot 9135. Option A is correct.