Question

Information on a packet of​ seeds, which may not be a random sample of​ seeds, claims that the germination rate is 94​%. ​What's the probability that more than 96​% of the 220 seeds in the packet will​ germinate? Be sure to discuss your assumptions and check the conditions that support your model.

Answer 1

0.1052

Explanation:

Given that proportion of germination in the population is 94% =0.94

p = 0.96

Sample size = 220

Std dev of p =
`\sqrt{(pq)/(n) } \\=0.016`

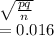
The probability that more than 96​% of the 220 seeds in the packet will​ germinate

=
`P(p\geq 0.96)\\=P(Z\geq (0.96-0.94)/(0.016))\\=P(Z\geq 1.25)\\==1-0.8948\\=0.1052`

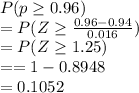
Assumptions are np and nq >5 and also sample size >220 hence normal