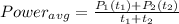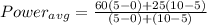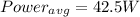Question

One cycle of the power dissipated by a resistor ( R = 800 Ω R=800 Ω) is given by P ( t ) = 60 W , 0 ≤ t < 5.0 s P(t)=60 W, 0≤t<5.0 s P ( t ) = 25 W , 5.0 ≤ t < 10 s P(t)=25 W, 5.0≤t<10 s This periodic signal repeats in both directions of time. What is the average power dissipated by the 800- Ω Ω resistor?

Answer 1

42.5W

Step-by-step explanation:

To solve this problem we must go back to the calculations of a weighted average based on the time elapsed thus,

`Power_(avg) = (P_1(t_1)+P_2(t_2))/(t_1+t_2)`

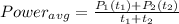
We need to calculate the average power dissipated by the 800\Omega resistor.

Our values are given by:

`P(t)=60 W, 0\leq t<5.0s`

`P(t)=25 W, 5.0\leq t<10s`

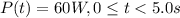
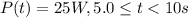
Aplying the values to the equation we have:

`Power_(avg) = (P_1(t_1)+P_2(t_2))/(t_1+t_2)`

`Power_(avg) = (60(5-0)+25(10-5))/((5-0)+(10-5))`

`Power_(avg) = 42.5W`