Question

Find all the 0's of this equation
-3x^4+27x^2+1200=0

Answer 1

The zeroes of the equation 4i,-4i,5,-5

Step-by-step explanation:

Given:

`-3x^4+27x^2+1200=0`

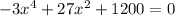
To Find:

The 0's of the equation=?

Solution:

We can write the equation by taking minus sign common from left hand side and the equation will become

`3x^4-27 x^2-1200=0`

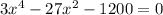
Now, Let
`x^2=t`

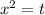
And put the value of
`x^2` in the above equation and then we will get

`3t^2-27t-1200=0`

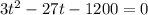
Now take 3 common from left hand side of the equation So equation would become

`t^2-9t-400=0`

`(x+16)(x-25)=0`

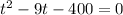
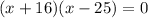
hence the roots are t= -16 and 25

Now that we know the value(s) of t , we can calculate x since x is
`√(t)`

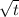
Since we are speaking 2nd root, each of the two imaginary solutions of has 2 roots

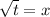
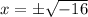
`√(t)= x`

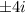
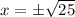
`x=\pm√(-16)`

x=
`\pm4i`

`x=\pm√(25)`

x=
`\pm5`

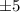
Hence the roots are 4i,-4i,5,-5