Question

Determine the magnetic flux through a circular surface (a disk) of radius 1.0 cm in a uniform magnetic field of 0.01 T when:

flux_fig1

The surface is oriented as shown at right top?



The surface is oriented at 45º to the magnetic field as shown at right middle?



The surface's normal vector is oriented perpendicular to magnetic field as shown at right bottom?

Answer 1

see explanation

Step-by-step explanation:

Magnetic flux is defined by
`\Phi = \int \vec{B} \cdot d\vec{A}`

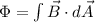
we have a disk with cross-section area
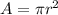`A = \pi r^2`, where
`r` is the radius of the disk ( r = 0.01 [m] ).

a) disk is perpendicular to the magnetic field

We assume the magnetic field is coming from the bottom, therefore
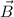`\vec{B}` and
`d\vec{A}` are parallel and the dot product is maximum because the angle between the vectors is 0.

the magnetic flux takes the following form:

`\Phi = \int \vec{B} \cdot d\vec{A}=\int B*dA*cos(0)=\int B*dA`

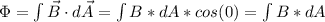
now the magnitude of B is constant, we have:

`B\int dA`

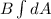
remember what
`A` is? then we just derivate it with respect to the radius and we get

`dA = (d )/(dr)(\pi r^2)=2\pi rdr`

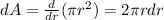
the flux now is
`\Phi=\B\int dA=B \int 2\pi rdr=2\pi B\int rdr= 2\pi B((r^2)/(2))=\pi Br^2`

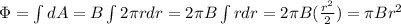
we just demonstrated that the flux of a magnetic field whose direction and magnitude are constant is equal to B times the area A of the surface the magnetic field is passing through:

now we replace values

`\Phi = 0.01 [T] * \pi *(0.01)^2=\pi *10^(-6)`

b) Now if the surface is oriented at 45° we go back a few steps and we just have a small difference this time:

`\Phi = \int \vec{B} \cdot d\vec{A}=\int B*dA*cos(45)=\pi*B*r^2*cos(45)`

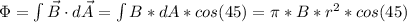
therefore

`\Phi = 0.01 [T] * \pi *(0.01)^2*cos(45)=\pi *10^(-6)*(1)/(√(2))`

the magnetic flux has decreased because of the incidence angle

c) if the surface vector is perpendicular to the magnetic field then the expression takes the following form:

`\Phi = \int \vec{B} \cdot d\vec{A}=\int B*dA*cos(90)=\pi*B*r^2*0 = 0`

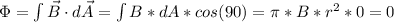
there is no magnetic flux because the thin disk is perpendicular to the magnetic field