Question

TV broadcast antennas are the tallest artificial structures on Earth. In 1987, a 69.0 kg physicist placed himself and 400 kg of equipment at the top of one 610 m high antenna to perform gravity experiments. By how much (in mm) was the antenna compressed, if we consider it to be equivalent to a steel cylinder 0.175 m in radius?

Answer 1

see description

Step-by-step explanation:

This is a problem where we have to assume we are in the linear region of the stress-strain curve for the antenna.

The physicist has a mass of 69 [Kg] and his equipment has a mass of 400 [Kg].

Now we just have to add those up, we end up with a mass of 469 [Kg].

The force exerted to the antenna (downwards) will be:

`F = 469 [Kg] * 9.8 [m/s^2]=4956.2 [N]`

To find the compression we have that the relationship between strain we take the equation:

`\gamma = (F*l_(o))/(A* \epsilon)`

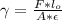
where
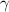`\gamma` is the young modulus,
`\epsilon` is the strain on the material,
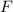`F` is the force exerted by the physicist+equipment,
`A` is the cross-section area of the cylinder, and
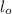`l_(o)` is the initial longitude of the cylinder.

now the young modulus for steel is
`\gamma = 200*10^9 [Pa]`.

The cross section area for the cylinder is
`A = \pi *r^2 = \pi *(0.175)^2=0.0962[m^2]`

The length of the antenna is
`l_(0)=610 [m]`

we find
`\epsilon`:

`\epsilon = (F*l_(o))/(A* \gamma)=(4956.2*610)/(0.0962*200*10^9) = 0.000157 [m] = 0.157 [mm]`