Question

Fairfield Homes is developing two parcels near Pigeon Fork, Tennessee. In order to test different advertising approaches, it uses different media to reach potential buyers. The mean annual family income for 13 people making inquiries at the first development is $151,000, with a standard deviation of $41,000. A corresponding sample of 28 people at the second development had a mean of $183,000, with a standard deviation of $28,000. Assume the population standard deviations are the same.

1.
State the decision rule for .10 significance level: H0: μ1 = μ2; H1:μ1 ≠ μ2. (Negative amounts should be indicated by a minus sign. Round your answers to 3 decimal places.)

Answer 1

Explanation:

Hello!

You want to compare two populations to see if there is a difference in the average annual income of the studied families.

H₀:μ₁ = μ₂

H₁:μ₁ ≠ μ₂

α: 0.10

Since the two samples are less than 30, I'll make the propper asumptions and use a Student t statistic to test the hypothesis.

t = (x₁[bar]-x₂[bar]) - (μ₁ - μ₂)

`\sqrt{S²_(1)/n_(1) + S²_(2)/n_(2)}`

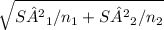
This distribution has
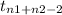`t_(n1+n2-2)` degrees of freedom.

The rejection region for this hypothesis set is two-tailed, this means, you will reject the null hypothesis if the statistic takes small values or big values. There are two critical values.

`t_(13+28-2;\0.10/2 )` =
`t_(39;\0.05 )` = -1.6849 ≅ -1.68

`t_(13+28-2;\1-(0.10/2) )` =
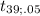`t_(39;\0.95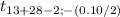)` = 1.6849 ≅ 1.68

So you'll rejec the null hypothesis if the calculated statistic is t ≤ -1.68 or t ≥ 1.68.

Sample 1

n₁ = 13

Mean (x₁[bar] = $151,000

S₁ = $41,000

Sample 2

n₂ = 28

Mean (x₂[bar] = $183,000

S₂ = $28,000

t = (151,000-183,000) - (0)

`√((41,000)²/13 + (28,000)²/28)`

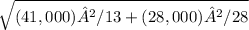
t = -32,000 = -2.551

12542.24

Since -2.551 is less than -1.68, you have significant evidence to reject the null hypothesis. The average annual income of the population 1 is different than the average annual income of the the population 2.