Answer:
The area of the floor of the shed is 1500 square feet.
Explanation:
Given:
The vertices of the floor of a shed are: (20,80), (50,60), (50,20) and (20,20)
Let us plot the given vertices on a graph.
From the graph, it is clear that the given figure is a trapezium with opposite parallel sides being parallel to the y axis. The height of the trapezium is the side that is parallel to x axis.
The area of the trapezium ABCD is given as:
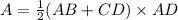
From the graph, AB = 60 ft, CD = 40 ft, AD = 30 ft
Therefore, the area is given as:
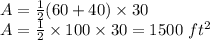
Therefore, the area of the floor of the shed is 1500 square feet.