Question

A university is conducting a survey in order to estimate the results of an upcoming local election. They intend to take a simple random sample of individuals from the population of eligible voters. Each selected individual will be asked whether they will vote for Candidate A, yes or no. The university intends to use the results to create a 95% CI for the population proportion of voters who will vote for Candidate A. They desire the interval to have a half-width of no more than 0.03. How many individuals must they sample? (Hint: the half-width of a CI for a population proportion is maximized when the sample proportion is set to p = 0.5.)

Answer 1

Answer: 1068

Explanation:

• Formula to find the same size :

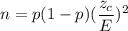`n= p(1-p)((z_c)/(E))^2` , where p is the prior population proportion , E is the margin of error and
`z_c` is the z-value at a certain confidence level.

As per given , we have

Margin of error at 95% confidence interval : E= half width of the confidence interval = 0.03

z-value for 95% confidence interval :
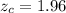`z_c=1.96` [using z-value table.]

Since no prior population proportion is given , so we take p= 0.5

[∵ the half-width of a CI for a population proportion is maximized when the sample proportion is set to p = 0.5. ]

Then , the sample size would be :-

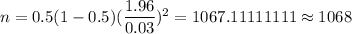`n= 0.5(1-0.5)((1.96)/(0.03))^2=1067.11111111\approx1068` [Rounded to the next integer.]

∴ They must sample 1068 individuals.