Responder:
El tiempo que toma A para completar el trabajo solo es de 20 días.
Explicación paso a paso:
datos proporcionados:
Tiempo que tarda (A + B) en terminar el trabajo = 12 days.
Deje que A A le tome tiempo completar el trabajo solo = x
entonces el tiempo que B tomó para completar el trabajo solo = x+10
1 día de trabajo de A + B =
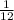
1 día de trabajo de A =
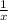
1 día de trabajo de B =
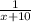
1 día de trabajo de A = {(
1 día de trabajo de A + B} - {1 día de trabajo de B}
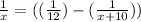
Resolviendo la ecuación que obtenemos.
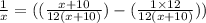
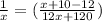
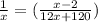
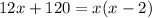
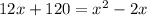
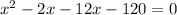
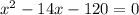
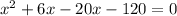
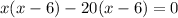
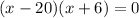
Ahora resolviendo 2 valores de x obtenemos
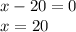
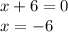
El número de días no puede ser negativo, por lo tanto, x = -6 no es válido
por lo tanto, el número de días que A puede completar el trabajo solo es de 20 días