Question

4th time posting this...........

Answer 1

D is the correct representation.

`((4x^2 + 2x)/(x^(2)+x-2) )/( (8x^2 +4x)/(3x^2 +10x+8) )` =
`{((3x+4))/(2(x-1))`

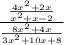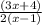
Explanation:

Here, the given equation is:

`((4x^2 + 2x)/(x^(2)+x-2) )/( (8x^2 +4x)/(3x^2 +10x+8) )`

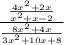
here, numerator =
`{(4x^2 + 2x)/(x^(2)+x-2) }`

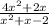
and denominator =
`(8x^2 +4x)/(3x^2 +10x+8)`

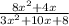
Solving numerator and denominator separately, we get

NUMERATOR:

`{(4x^2 + 2x)/(x^(2)+x-2) } \implies(2x(2x +1))/(x^(2) + 2x-x-2 ) \\\implies(2x(2x +1))/((x+2)(x-1) )`

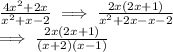
Denominator:

`(8x^2 +4x)/(3x^2 +10x+8)  = (4x(2x+1))/(3x^2 +6x+ 4x+8)\\ \implies (4x(2x+1))/(3x(x+2)+ 4(x+2))  =  (4x(2x+1))/((3x+4)(x+2))`

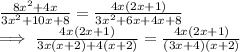
Hence, the transformed fraction is:

`((2x(2x +1))/((x+2)(x-1) ))/((4x(2x+1))/((3x+4)(x+2)))  = {(2x(2x +1))/((x+2)(x-1) )} *{((3x+4)(x+2))/(4x(2x+1))`

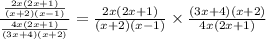
or, implied fraction is
`{((3x+4))/(2(x-1))`

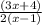
Hence, D is the correct representation.