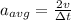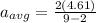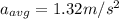Answer:
Part a)
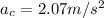
Part b)
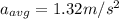
Step-by-step explanation:
As we know that it makes half revolution in given time interval
so we have
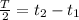
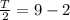
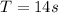
now the angular speed is given as
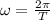
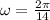

now linear speed is given as

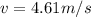
now we have
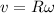
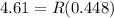
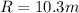
Now centripetal acceleration is given as
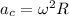
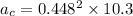
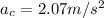
Part b)
Average acceleration of the cat is given as