Question

What are the coordinates of the circumcenter of this triangle? Enter your answer in the boxes.

Coordinates of points:
A(-1, 5) | B(-1, -3) | C(5, 3)

Answer 1

(2,1)

Explanation:

We can see that the given triangle.

The coordinates of A are (-1,5) .

The coordinates of B are (-1,-3).

The coordinates of C are (5,-3).

Distance formula:
`√((x_2-x_1)^2+(y_2-y_1)^2)`

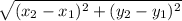
AB=
`√((-3-5)^2+(-1+1)^2)=8` units

BC=
`√((5+1)^2+(-3+3)^2)=6` units

AC=
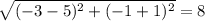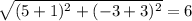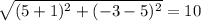`√((5+1)^2+(-3-5)^2)=10` units

Pythagoras theorem:
`(Hypotenuse)^2=(Base)^2+(Perpendicular\;side)^2}`

`AB^2+BC^2=8^2+6^2=100`

`AC^2=(10)^2=100`

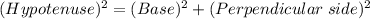
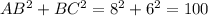
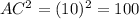
Therefore,
`AC^2=AB^2+BC^2`

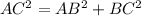
When a triangle satisfied the Pythagoras theorem then, the triangle is right triangle.

Hence, the given triangle is a right triangle.

We know that circum-center of right triangle is the mid point of hypotenuse.

Mid-point formula:
`x=(x_1+x_2)/(2),y=(y_1+y_2)/(2)`

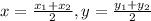
Using this formula then, we get

Mid-point of hypotenuse AC is given by

`x=(-1+5)/(2)=2,y=(5-3)/(2)=1`

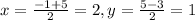
Hence, the circum-center of triangle is (2,1).