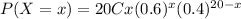Answer:
0.7553
Explanation:
Given that in a busy coffee shop, which is a member of an international chain of coffee shops, 40% of customers order a pastry in addition to their drink.
Hence for 20 customers selected at random during one business day, x the no of customers who did not order a pastry with their drink is binomial since each customer is independent and there are only two outcomes.
X is binomial with n =20 and p = 1-0.4 = 0.60
q = 0.4
the probability that at least 11 of them did not order a pastry with their drink
=
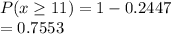
Note that binomial prob