Answer:
The error bound is 3.125%.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence interval
, and a confidence interval
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
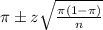
In which
z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
A sample of 506 California adults.. This means that
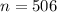 .
.
76% of California adults (385 out of 506 surveyed) feel that education is one of the top issues facing California. This means that
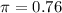
We wish to construct a 90% confidence interval
So
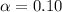 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
 , so
, so
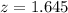 .
.
The lower limit of this interval is:

The upper limit of this interval is:
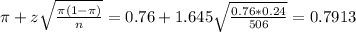
The error bound of the confidence interval is the division by 2 of the subtraction of the upper limit by the lower limit. So:
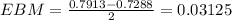
The error bound is 3.125%.