Question:
Matt and Ming are selling fruit for a school fundraiser. Customers can buy small boxes of oranges and large boxes of oranges. Matt sold 3 small(?) boxes of oranges and 14 large boxes of oranges for a total of $203. Ming sold 11 small boxes of oranges and 11 large boxes of oranges for a total of $220. Find the cost each of one small box of oranges and one large box of oranges.
Answer:
Cost of one small box is $7 and cost of one large box is $13
Explanation:
Given:
Cost of 11 small boxes and 11 large small boxes of oranges sold by Ming=$220
Cost of 3 small boxes and 14 large small boxes of oranges sold by Matt=$203
To Find:
Cost of one small orange box=?
Cost of one large orange box=?
Solution:
Let the cost of one small box be $a
Cost of one big box be $b.
Matt sold 3 small boxes of oranges and 14 large boxes of oranges for a total of $203
Then,
3 x $a + 14 x $b = $203
3a + 14b = 20………………………………..(1)
Ming sold 11 small boxes of orange and 11 large boxes of orange for a total of $220.
Then,
11 x $a + 11 x $b = $220
11a + 11b = 220
a + b = 20……………………………………(2)
Now, solving the above equations,
From equation(2) we get
a = 20 – b
So, put value of a in (1)
3(20 – b) + 14b = 203
60 – 3b + 14b = 203
11b = 203 – 60
11b = 143
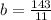
b=13
Thus,
a = 20 – 13 = 7
a=7