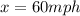Question

Assume that the operating cost of a certain truck (excluding driver's wages) is 12+x/6 cents per mile when the truck travels at x mi/hr. If the driver earns $6 per hour, what is the most economical speed to operate the truck on a 400 mi turnpike where the minimum speed is 40 mph and the maximum speed is 70 mph?

Answer 1

`x = 60 mph`

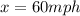
Step-by-step explanation:

Given that the operating cost is

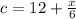`c = 12 + (x)/(6)` cents per mile

total miles covered is given as

`d = 400 miles`

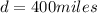
so total cost of drive is given as

`C = (12 + (x)/(6))(4)` $

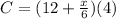time taken by the truck to move the distance is given as

`t = (400)/(x)`

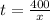
So total earnings of the driver is given as

`E = (400)/(x) * 6` $

now total profit of the driver is given as

`P = (2400)/(x) - (48 + (2x)/(3))` $

to maximize the profit we have

`(dP)/(dx) = 0`

`-(2400)/(x^2) + (2)/(3) = 0`

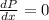
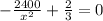
so we have

`x = 60 mph`