Answer:
The 95% confidence interval of the true proportion of all Americans who are in favor of gun control legislation is (0.5471, 0.5779).
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence interval
, and a confidence interval
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
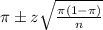
In which
z is the zscore that has a pvalue of
 .
.
For this problem, we have that:
A random sample of 4000 citizens yielded 2250 who are in favor of gun control legislation. This means that
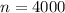 and
and
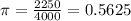
Estimate the true proportion of all Americans who are in favor of gun control legislation using a 95% confidence interval
So
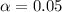 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
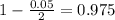 , so
, so
 .
.
The lower limit of this interval is:
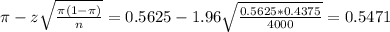
The upper limit of this interval is:
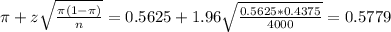
The 95% confidence interval of the true proportion of all Americans who are in favor of gun control legislation is (0.5471, 0.5779).