Answer:
0.8647,0.5940
Explanation:
Given that a chromosome mutation believed to be linked with colorblindness is known to occur, on the average, once in every 10,000 births.
Hence for a sample of 20000 babies we can take average as 2.
2) Since n is very large and p is small but np is finite Poisson model applies here.
1) the probability that at least one will develop colorblindness
=
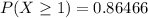
3) the probability that 2 or more babies will develop colorblindness, using the appropriate Poisson model.
=
