Question

There are two machines available for cutting corks intended for use in wine bottles. The first produces corks with diameters that are normally distributed with mean 3 cm and standard deviation 0.08 cm. The second machine produces corks with diameters that have a normal distribution with mean 3.04 cm and standard deviation 0.02 cm. Acceptable corks have diameters between 2.9 cm and 3.1 cm.

1. What is the probability that the first machine produces an acceptable cork? (Round your answer to four decimal places.)

Answer 1

Answer: 0.7887

Explanation:

Let x be the random variable that represents the diameters of the corks .

Given : The first produces corks with diameters that are normally distributed with mean 3 cm and standard deviation 0.08 cm.

i.e.
`\mu=3\ cm\ \ ,\sigma=0.08\ cm`

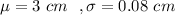
Acceptable corks have diameters between 2.9 cm and 3.1 cm.

Then, the probability that the first machine produces an acceptable cork will be :_

`P(2.9<x<3.1)=P((2.9-3)/(0.08)<(x-\mu)/(\sigma)<(3.1-3)/(0.08))\\\\=P(-1.25<x<1.25)\\\\=1-2P(z>1.25)\ \ [\because\ P(-z<Z<z)=1-2P(Z>|z|)]\\\\=1-2(1-P(z<1.25))\ \ [\because\ P(Z>z)=1-P(Z<z)]\\\\=1-2(1-0.8943502)\\\\=1-2(0.1056498)=0.7887004\approx0.7887`

∴ The probability that the first machine produces an acceptable cork= 0.7887