Answer: 0.7887
Explanation:
Let x be the random variable that represents the diameters of the corks .
Given : The first produces corks with diameters that are normally distributed with mean 3 cm and standard deviation 0.08 cm.
i.e.
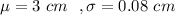
Acceptable corks have diameters between 2.9 cm and 3.1 cm.
Then, the probability that the first machine produces an acceptable cork will be :_
![P(2.9<x<3.1)=P((2.9-3)/(0.08)<(x-\mu)/(\sigma)<(3.1-3)/(0.08))\\\\=P(-1.25<x<1.25)\\\\=1-2P(z>1.25)\ \ [\because\ P(-z<Z<z)=1-2P(Z>|z|)]\\\\=1-2(1-P(z<1.25))\ \ [\because\ P(Z>z)=1-P(Z<z)]\\\\=1-2(1-0.8943502)\\\\=1-2(0.1056498)=0.7887004\approx0.7887](https://img.qammunity.org/2020/formulas/mathematics/college/z7ypt1j529pm42q14q2zquxdx2nsc27wx8.png)
∴ The probability that the first machine produces an acceptable cork= 0.7887