Answer:
The chain of supermarkets must order 428.1 gallons of milk.
Explanation:
Let's define the random variable X.
X : ''Weekly volume of sales in thousands of gallons''
X is a continuous random variable.
The probability density function for X is
 when 0 < x < 1
when 0 < x < 1
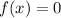 Otherwise.
Otherwise.
Let's denote as ''a'' to the quantity of milk for the question.
We are looking for :
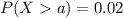
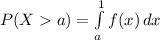
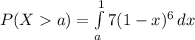
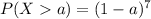
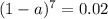
![a=1-\sqrt[7]{0.02}](https://img.qammunity.org/2020/formulas/mathematics/college/7731ebembh31pjefge2nej0a11ew7s5j64.png)
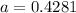
a is in thousands of gallons, therefore the chain of supermarkets must order
428.1 gallons of milk in order to satisfy the question.