Step-by-step explanation:
In order to prove that f is one-to-one and surjective, we can prove directly that f is bijective by findng
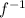 .
.
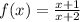
To calculate the inverse of f, first we swap the variables x and y. Then we write y in values of x.
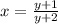
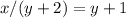
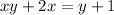
On this step it is important to separate what terms contain y and what terms do not. After that we can separate y as a factor
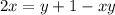
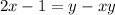
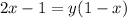
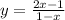
Thus,
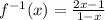 . Note that
. Note that
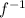 is well defined en every element of B, because it can be defined on any element different from 1, where the divider is zero.
is well defined en every element of B, because it can be defined on any element different from 1, where the divider is zero.
An element of the form
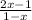 , for some x, is an element of A because it is different from -2. Lets suppose that there exist an x such as
, for some x, is an element of A because it is different from -2. Lets suppose that there exist an x such as
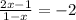 , thus 2x-1 = -2(1-x) = -2+2x, from where we conclude that 0 = -1, that is a contradiction. As a result,
, thus 2x-1 = -2(1-x) = -2+2x, from where we conclude that 0 = -1, that is a contradiction. As a result,
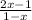 cant be equal to -2.
cant be equal to -2.
I hope this works for you!