The given system of equation that is
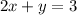 and
and
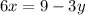 has infinite number of solutions.
has infinite number of solutions.
Option -C.
Solution:
Need to determine number of solution given system of equation has.
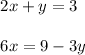
Let us first bring the equation in standard form for comparison

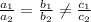
To check how many solutions are there for system of equations
 , we need to compare ratios of
, we need to compare ratios of
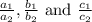
In our case,
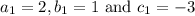
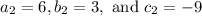
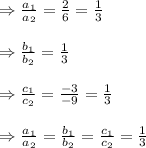
As
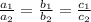 , so given system of equations have infinite number of solutions.
, so given system of equations have infinite number of solutions.
Hence, we can conclude that system has infinite number of solutions.