Question

A child's top is held in place upright on a frictionless surface. The axle has a radius of ????=3.21 mm . Two strings are wrapped around the axle, and the top is set spinning by applying T=3.15 N of constant tension to each string. If it takes 0.320 s for the string to unwind, how much angular momentum does the top acquire? Assume that the strings do not slip as the tension is applied.

Answer 1

Angular momentum,
`L=6.47* 10^(-3)\ m`

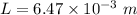
Step-by-step explanation:

It is given that,

Radius of the axle,
`r=3.21\ mm=3.21* 10^(-3)\ m`

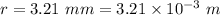
Tension acting on the top, T = 3.15 N

Time taken by the string to unwind, t = 0.32 s

We know that the rate of change of angular momentum is equal to the torque acting on the torque. The relation is given by :

`\tau=(dL)/(dt)`

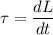
Torque acting on the top is given by :

`\tau=F* r`

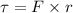
Here, F is the tension acting on it. Torque acting on the top is given by :

`\tau=2F* r`

`2T* r=(L)/(t)`

`L=2T* r * t`

`L=2* 3.15* 3.21* 10^(-3)* 0.32`

`L=6.47* 10^(-3)\ m`

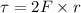
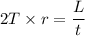
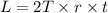
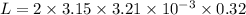
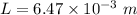
So, the angular momentum acquired by the top is
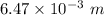`6.47* 10^(-3)\ m`. Hence, this is the required solution.