Answer:
A. The graph of
 is the graph of
is the graph of
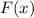 stretched vertically, flipped over the x axis, and shifted 7 units down.
stretched vertically, flipped over the x axis, and shifted 7 units down.
Explanation:
Given:
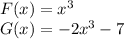
In order to transform
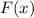 to
to
 , we need to follow the following transformation rules:
, we need to follow the following transformation rules:
1. Multiply the function by the number 2. According to transformation rules, multiplying a function by a positive number greater than 1 results in vertical stretch of the function's graph.
2. Multiply by -1. Multiplying a function by -1 flips it over the x axis.
3. Add -7 to the function obtained in step 2. When a negative number C is added to a function, then the graph shift down by C units. So, here the graph shifts down by 7 units.
Thus, the graph of
 is the graph of
is the graph of
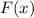 stretched vertically, flipped over the x axis, and shifted 7 units down.
stretched vertically, flipped over the x axis, and shifted 7 units down.