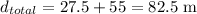Question

An athlet starting from stationary moves with an acceleration 2.2m/s^2 for 5 seconds, then for other 5 seconds

continues with steady speed up to the finish line.
-Arrange in a graph Speed due to time.
-What is the athlet's speed when crossing the finish line?
-Calculate the distance covered from start till the finish line.​

Answer 1

The graph is shown below.

The athlete's speed at the finish line is 11 m/s

Total distance covered is 82.5 m.

Step-by-step explanation:

The graph of speed versus time is drawn below.

Acceleration in the first 5 seconds,
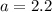`a=2.2` m/s²

From the graph, the slope of line OA is the acceleration in the first 5 seconds.

Slope of line OA is given as:

`slope, a=(AD)/(OD)\\2.2=(AD)/(5)\\AD =2.2* 5=11\textrm{ m/s}`

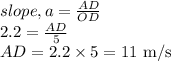
Now, the length AD is nothing but speed at point A or B as AB is a straight line.

Therefore, the speed when crossing the finish line is the speed at B which is equal to 11 m/s.

Distance covered is given by the total area under the graph.

The total area can be divided into two shapes; a triangle and a rectangle.

The area under the graph is the sum of areas of triangle OAD and rectangle ABCD.

Area of triangle OAD is,
`A_(tri)=(1)/(2)* OD* AD=(1)/(2)* 5* 11=27.5`

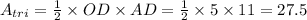
Area of rectangle ABCD is,
`A_(rec)=AB* AD=5* 11=55`

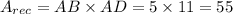
Therefore, the total distance covered till the finish line is given as:

`d_(total)=27.5+55=82.5\textrm{ m}`