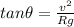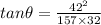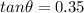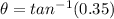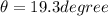Question

Suppose you are driving a car around in a circle of radius 157 ft, at a velocity which has the constant magnitude of 42 ft/s. A string hangs from the ceiling of the car with a mass of 1.8 kg suspended from it. What angle (in degrees) will the string make with the vertical?

Answer 1

`\theta = 19.3 degree`

Step-by-step explanation:

As we know that the car is moving in circular path with uniform speed

so the mass hanging on the string will experience the centrifugal force in radially outward direction in frame of motion of car

So at this position we can use force balance on the mass

let the string makes some angle with the vertical

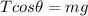`T cos\theta = mg` in vertical direction

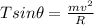`T sin\theta = (mv^2)/(R)` in radial direction

so here we will have by division of two equations

`tan\theta = (v^2)/(Rg)`

`tan\theta = (42^2)/(157* 32)`

`tan\theta = 0.35`

`\theta = tan^(-1)(0.35)`

`\theta = 19.3 degree`