Answer:
- 0.352
Explanation:
Data provided in the question:
Age (X) 50 34 12 36 18
(Y) 6.20 1.40 6.05 3.30 8.05
Now,
correlation coefficient, r =
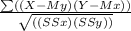
Here,
∑(X - Mx)² = SSx
∑(Y - My)² = SSy
Mx: Mean of X Values =
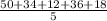 = 30
= 30
My: Mean of Y Values =
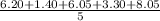 = 5
= 5
X - Mx & Y - My: Deviation scores
(X - Mx)² & (Y - My)²: Deviation Squared
(X - Mx)(Y - My): Product of Deviation Scores
Thus,
( X - Mx ) ( Y - My ) (X - Mx)² (Y - My)² (X - Mx)(Y - My)
20.0 1.20 400.0 1.44 24.0
4.0 -3.60 16.0 12.96 -14.4
- 18.0 1.05 324.0 1.102 -18.9
6.0 -1.70 36.0 2.89 -10.2
- 12.0 3.05 144.0 9.303 -36.6
-------------------------------------------------------------------------------------------------------
∑(X - Mx)² = 920.0
∑(Y - My)² = 27.695
∑(X - Mx)(Y - My) = -56.1
thus,
r =
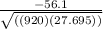
or
r = - 0.352