Question

Help whit that 3 questions please and thanks

Answer 1

80.

`4s+5c=46\\3s+c=22`

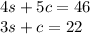
81. Each apple cost $0.50

82. One pound of chocolate = $3

Explanation:

80.

Let sold of 1 senior citizen ticket be "s", and

cost of 1 child ticket be "c"

First Day, 4 senior citizen ticket and 5 child tickets sold, equaled $46, so the equation we can write is:

`4s+5c=46`

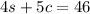
Second Day, 3 senior citizen ticket and 1 child ticket sold, equaled $22, so the equation we can write is:

`3s+c=22`

So, the system of equation (2 equations) written above can be solved simultaneously to find our answer.

`4s+5c=46\\3s+c=22`

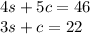
81.

Let price of 1 apple be "a" and price of 1 banana be "b"

Since 3 apples and 2 banana cost $2, so we can write:

3a + 2b = 2

Then,

4 apples and 4 bananas cost $3, so we can write:

4a + 4b = 3

We can solve for the variable b in equation 1. Shown below:

`3a + 2b = 2\\2b=2-3a\\b=(2-3a)/(2)`

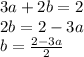
Now we put this value of b into equation 2 and solve for cost of 1 apple, a. Shown below:

`4a+4b=3\\4a+4((2-3a)/(2))=3\\4a+4-6a=3\\2a=1\\a=(1)/(2)\\a=0.5`

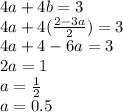
So each apples cost $0.5

82.

Let 1 pound of chocolate be cost "c"

Let 1 pound of peanut be cost "p"

4 lb of chocolate and 2 lb of peanut = $16, thus we can write:

4c + 2p = 16

Next,

2 lb of chocolate and 3 lb of peanut costed $12, so we can write:

2c + 3p = 12

We solve first equation for p:

`4c + 2p = 16\\2p=16-4c\\p=(16-4c)/(2)\\p=8-2c`

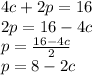
Now, we put this expression for p into equation 2 and solve for c:

`2c + 3p = 12\\2c + 3(8-2c) = 12\\2c+24-6c=12\\4c=12\\c=3`

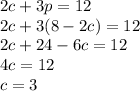
So, 1 pound of chocolates cost $3